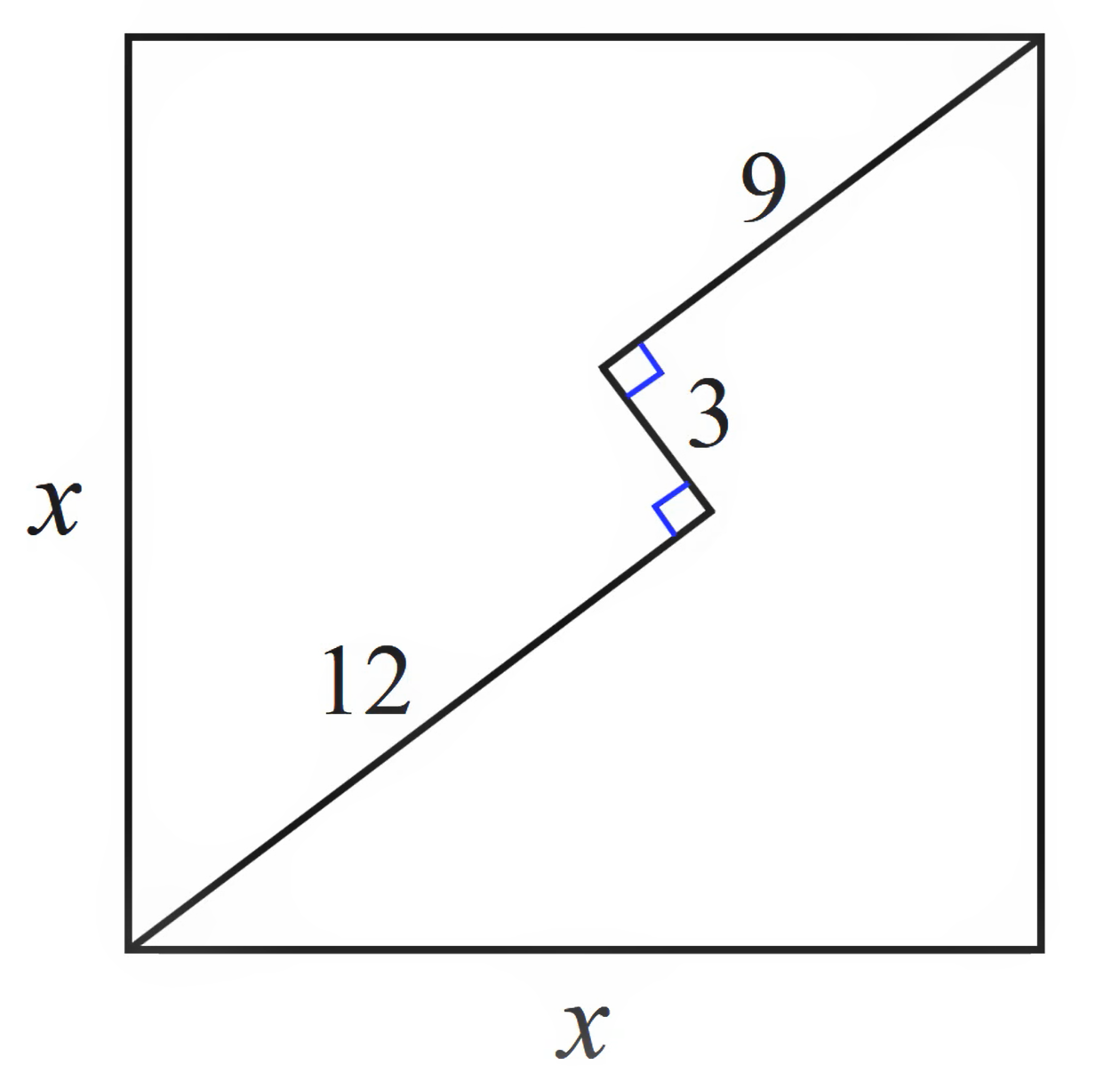
1. Il lato del quadrato

Trova la misura x del lato del quadrato. Gli angoli in blu sono retti.

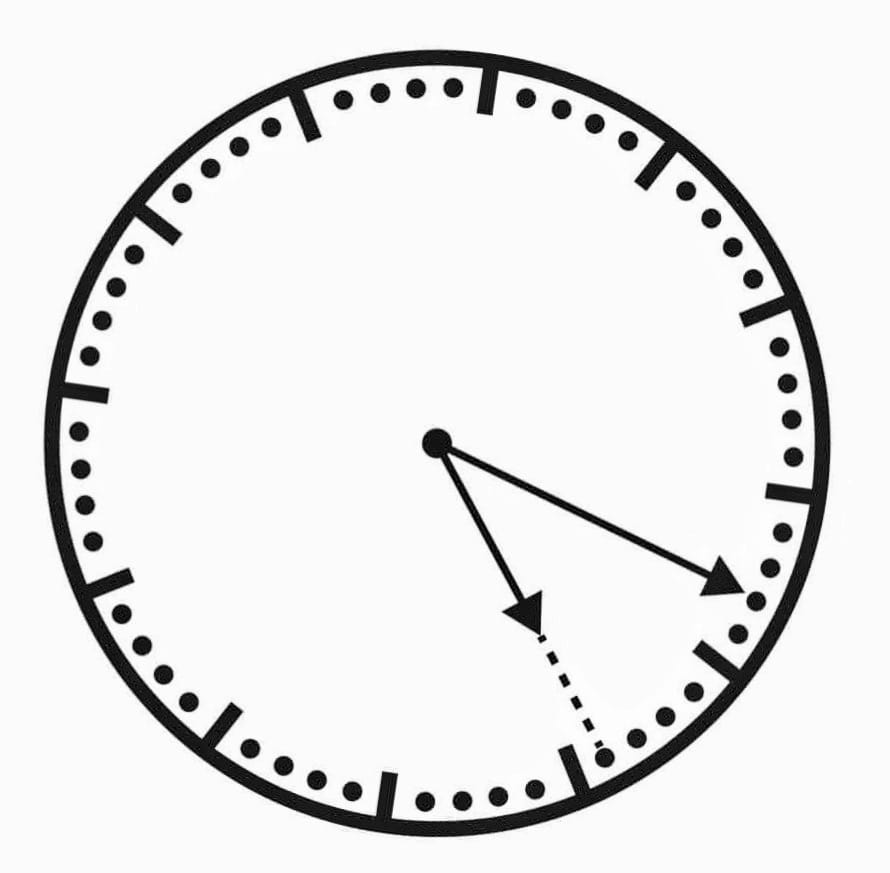
2. L'orologio girato

Un orologio senza numeri viene girato di un angolo a caso.
Che ora indica l'orologio?

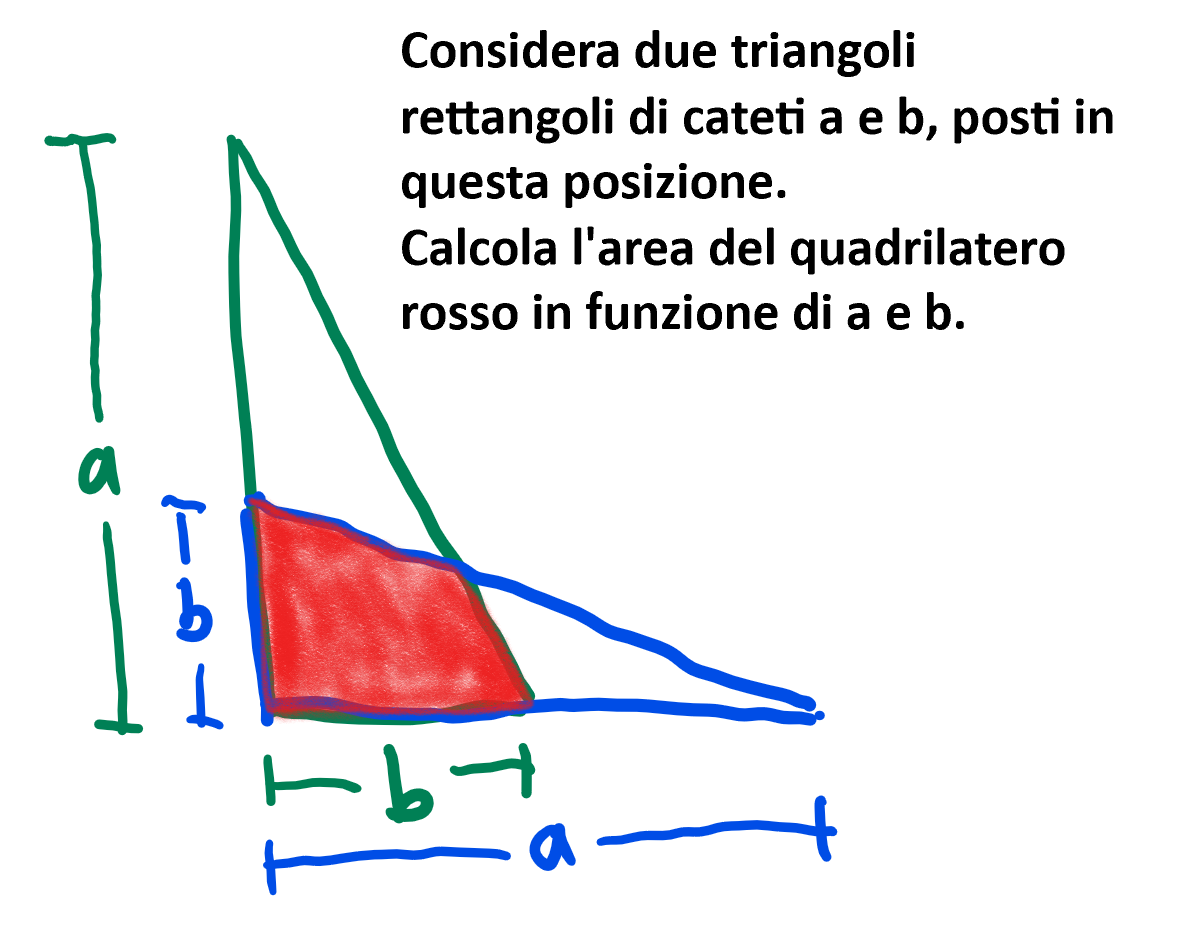
3. I due triangoli rettangoli

4. Le età dei figli (un classico)

La signora Sonia ha tre figli.
Il signor Vladimir chiede: "Che età hanno i suoi tre figli?"
"Il prodotto delle età dà 36, e la somma il numero del bus che sta passando ora."
Vladimir guarda il bus, ragiona un po' ed esclama: "Mi manca un dato!"
"Ha ragione", replica la signora Sonia, " il maggiore ha gli occhi azzurri!"
Vladimir a questo punto indovina le tre età. Quali sono?

5. Crittografia

Chi è l'autore del testo seguente?
(da me astutamente criptato)

“Ti qcgw qvs qcawbqwow o qodwfs qvs bcb gw dofzo gczoasbhs dsf dofzofs, dsf rwfs 'vc tohhc eisghc' 'vc tohhc eiszzc' 'vc aobuwohc s psjihc', ao gw dofzo dsf tofgw ib'wrso, dsf qodwfs qcas jo eisghc acbrc. Bcb qw ojsjc aow dsbgohc dfwao.”

6. QUIZ RIPRODUTTIVO

Una madre in questo momento ha esattamente 21 anni più del figlio.
Tra 6 anni l'età della madre sarà 5 volte quella del figlio.
Dov'è il padre in questo momento?

7. IL PONTE DI NOVOSIBIRSK

Yuri Gagarin, il principe Myškin, Aleksej Kirillovič Vronskij e Pierino devono attraversare un ponte.

Purtroppo sono al buio e possono disporre di una sola torcia (il ponte può essere attraversato solo con la torcia).
Inoltre solo due persone alla volta possono camminare sul ponte.

Considerando che i 4 impiegano rispettivamente 1, 2, 5 e 10 minuti per attraversare il ponte e che quando due lo attraversano insieme camminano alla velocità del più lento (cioè se Vladimir, 1 minuto, e Vronskij, 10 minuti, attraversando insieme impiegano 10 minuti, altrimenti uno dei due rimarrebbe al buio),
qual è il tempo minimo che necessitano per attraversare tutti e quattro il ponte?
(tutti e 4 devono trovarsi dall'altra parte del ponte)

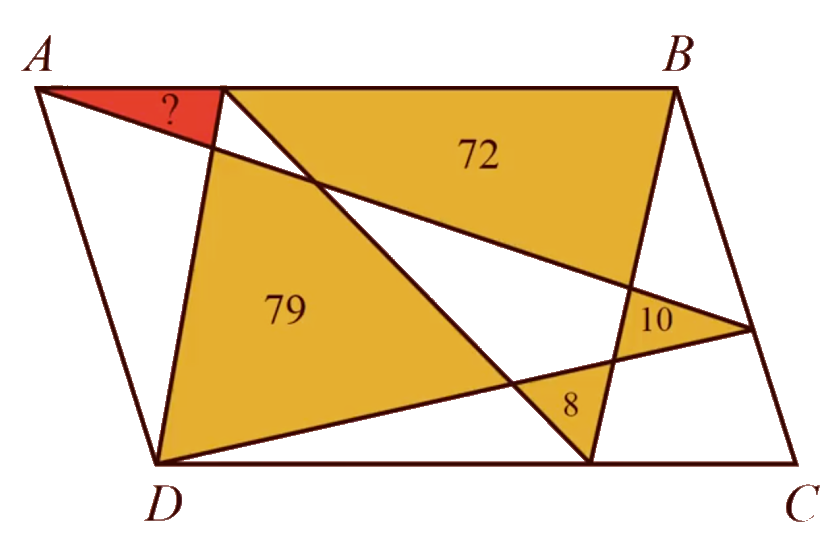
8. QUIZ DALLA CINA

ABCD è un parallelogrammo. I numeri rappresentano le aree dei vari poligoni. Il disegno non è in scala.
Trova l'area del triangolino rosso. (basta la matematica di prima media)

9. QUIZ KOLKHOZIANO

Ivan, Pyotr e Semyon e le loro mogli Olga, Irina e Anna hanno in tutto 151 anni.
Ogni marito ha 5 anni in più della moglie.
Ivan ha un anno in più di Irina.
Olga e Ivan hanno 48 anni assieme.
Semyon e Olga hanno 52 anni assieme.

Chi è sposato a chi e quanti anni hanno ognuno di loro?

10. ORO NERO

11. I MATEMATICI E IL DITTATORE

Leibniz e Erdös (entrambi geniali matematici) sono prigionieri di un feroce dittatore est-asiatico (un nome a caso, Kim), che minaccia di ferirli con un bazooka.

"Avrete salva la vita solo se risolverete il mio quiz: dovete trovare due numeri naturali compresi tra 1 e 100, 1 e 100 non compresi"

Poi Kim dice in segreto a Leibniz il prodotto dei due numeri, dicendogli che quello è il loro prodotto.
Poi Kim dice in segreto a Erdös la somma dei due numeri, dicendogli che quella è la loro somma.

I due riflettono un po', mentre Kim carica l'armamento.
"Ora potete parlare tra voi, ma senza nominare numeri."

Leibniz dice: "Non conosco il valore dei due numeri."
Erdös dice: "Lo sapevo che non lo sapevi. Non lo so nemmeno io."
Leibniz dice: "Ora so i due numeri."
Erdös dice: "Ora li so pure io."

Kim, deluso sfoga il bazooka al cielo, abbattendo un aereo USA che passava di li per caso.

Quali sono i due numeri?

12. Il compleanno di Nastassya Filippovna

Ozzy e Yuri hanno appena incontrato Nastassya, e Ozzy chiede a Nastassya : “Quand’è il tuo compleanno?”.
Nastassya ci pensa un attimo e dice: “Non te lo dico, ma ti posso dare qualche indizio”.
Prende un foglietto e scrive 10 date dicendo che il suo compleanno è una di quelle:

15 – 16 – 19 gennaio

17 – 18 febbraio

14 – 16 settembre

14 – 15 – 17 ottobre

Poi Nastassya sussurra all’orecchio di Ozzy il mese, e solo il mese, del suo compleanno.
A Yuri, invece, sussurra il giorno, e solo il giorno.

A questo punto Ozzy dice : "Non so quando sia il compleanno di Nastassya, ma so che neppure Yuri lo sa."
Yuri allora dice: “All’inizio non lo sapevo, ma ora sì”. E adesso anche Ozzy dice di saperlo.

Quindi, quand’è il compleanno di Nastassya Filippovna?

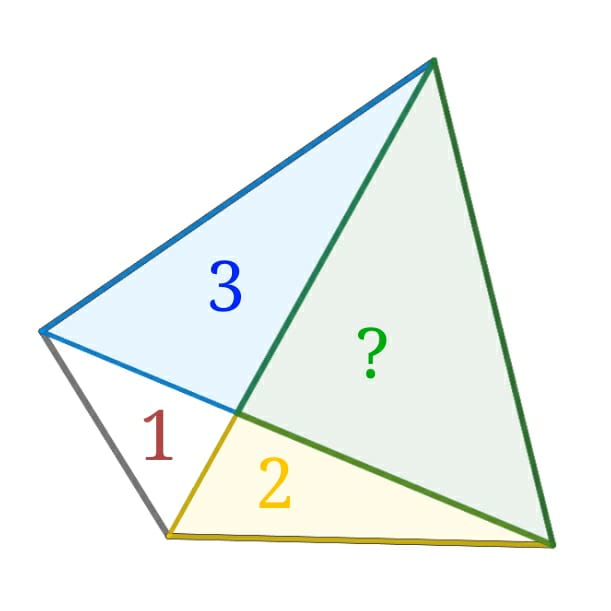
13. L'area sconosciuta

Quanto misura l'area "?" ? (1,2 e 3 sono le aree dei tre triangolini)

14. QUIZ ECOLOGICO

Vogliamo prendere tutta la plastica prodotta nel mondo nel 2017 e farne un'unico foglio spesso 1 mm.

Potremmo ricoprire tutta la superficie Helvetica con quel foglio?

(servono competenze matematiche di prima media)

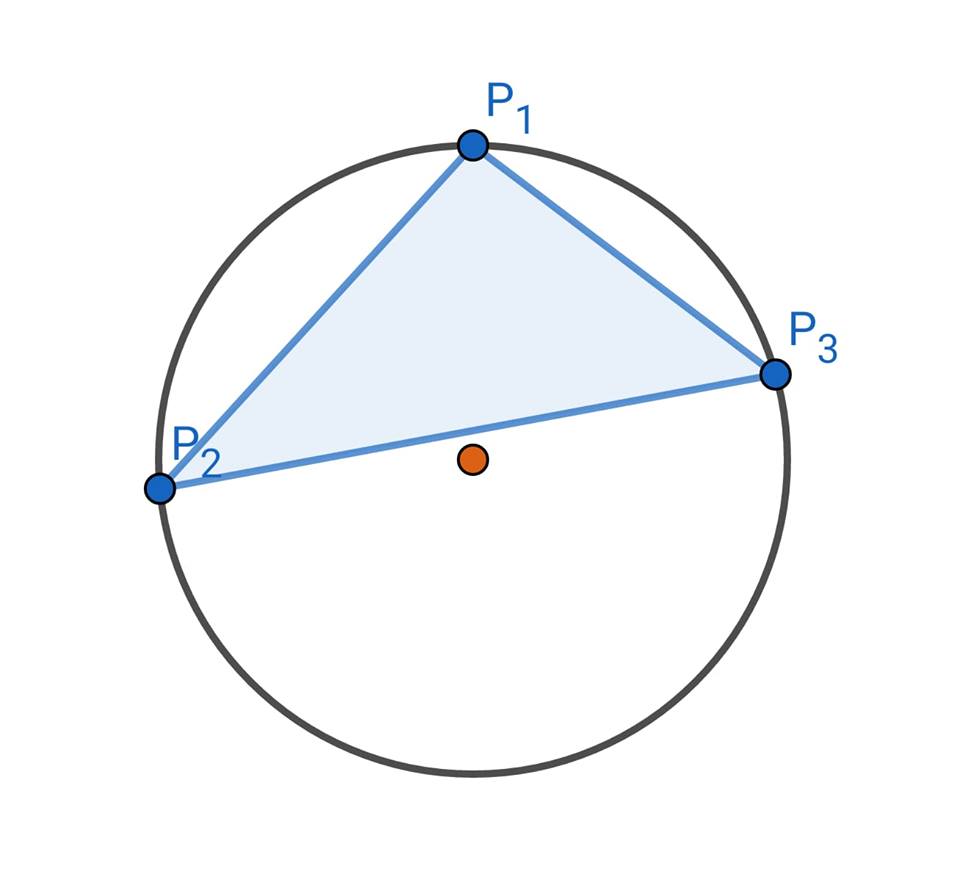
15. Triangolo nella circonferenza

Scegliete tre punti a caso su una circonferenza e uniteli formando un triangolo.

Qual è la probabilità che quel triangolo contenga il centro della circonferenza? 😁

16. La quaterna

Trova una quaterna di numeri naturali a, b, n, m > 1 che soddistano questa equazione.
Per quelli bravi: trovatene una seconda :-)

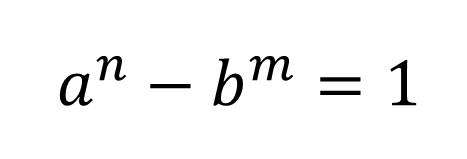
17. Il calendario

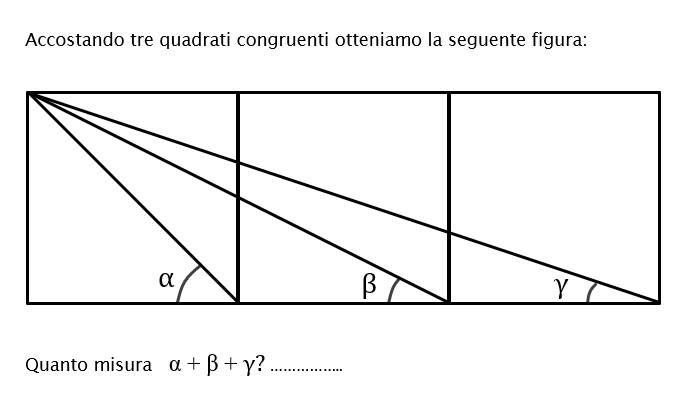
18. Somma di angoli

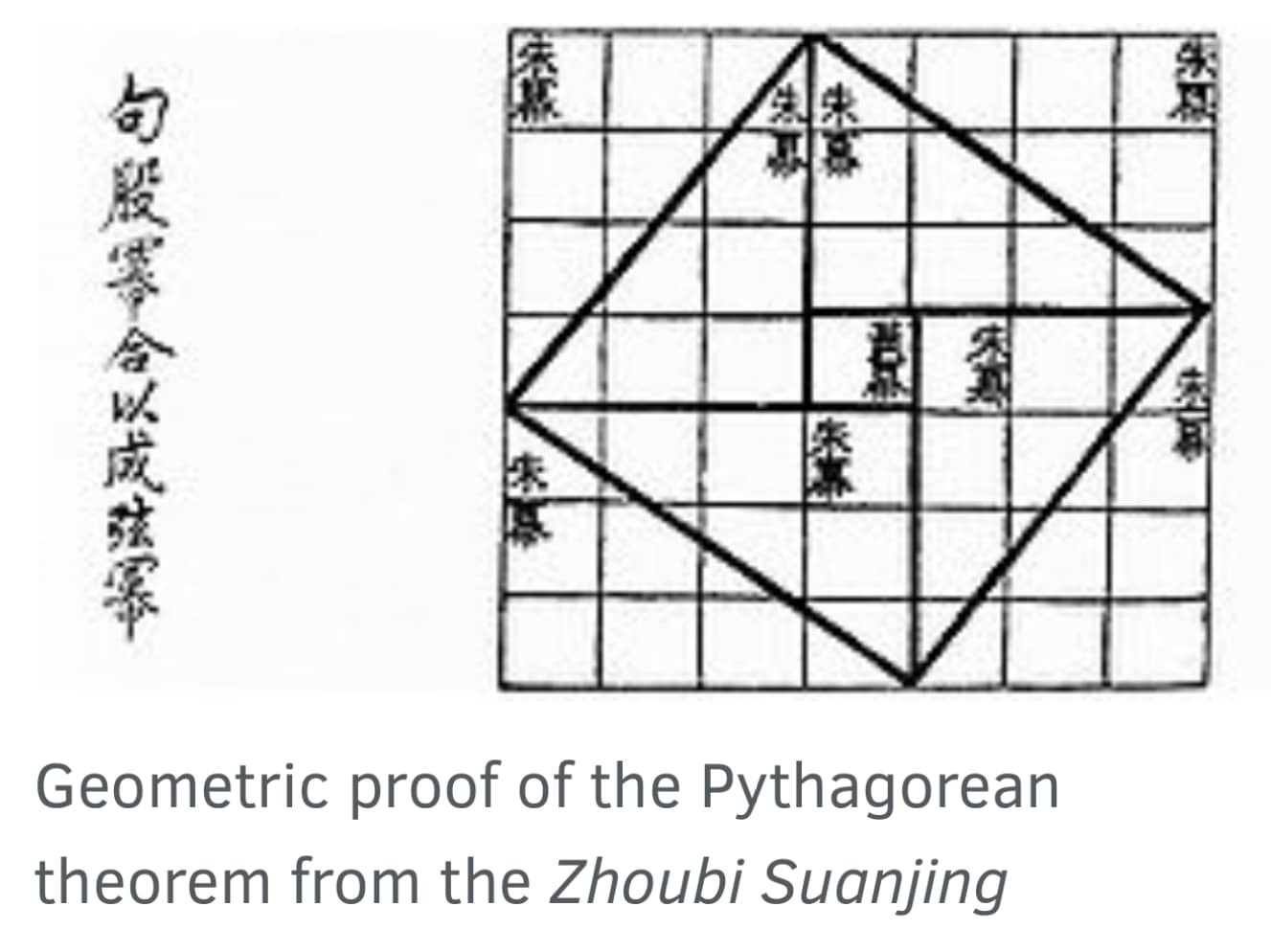
19. TERNE PITAGORICHE

615 è la misura dell'ipotenusa di 4 diversi triangoli rettangoli con cateti di misura intera.

a) Trova le misure dei cateti nei 4 casi.

b) Sai trovare un altro numero che ha questa particolarità?

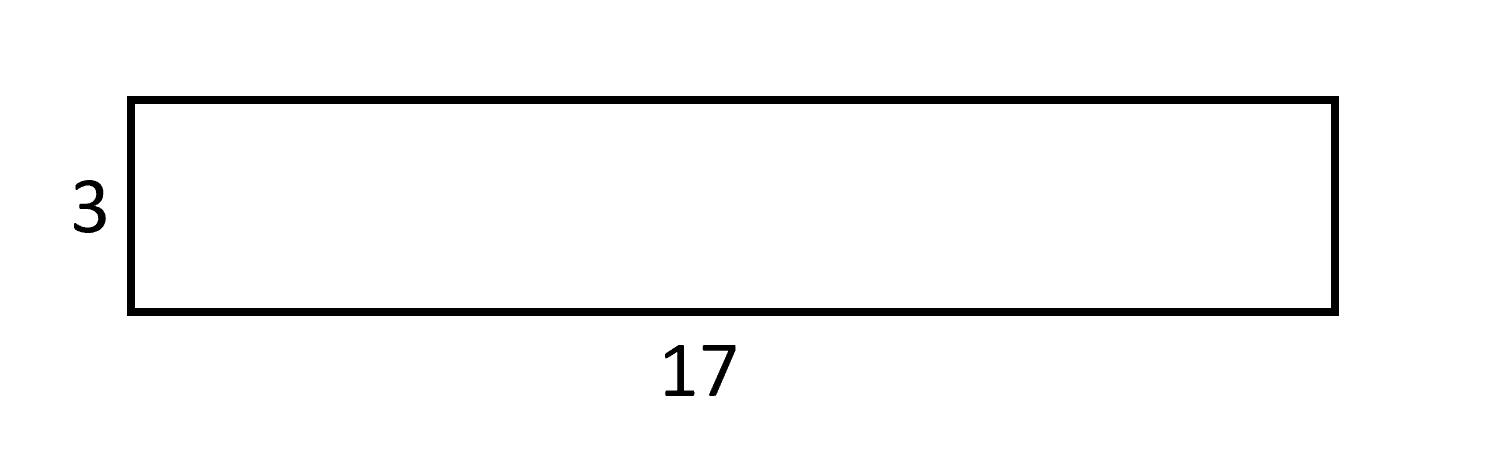
20. TOP SECRET :-)

Quanto misura l'area di questo rettangolo?

Area …….

21. SECONDA STELLA A DESTRA (Un classico di Sam Loyd)

In quest'immagine è nascosta una stella a 5 punte.
Riuscite a vederla?

22. L'ENERGIA CORRE VIA

Tutte le auto svizzere diventano elettriche all'istante.

Quante centrali idroelettriche come quella di Biasca servono per rifornirle?

23. Antico quiz babilonese

Presento questo quiz, principalmente per il suo significato storico.
Compare infatti sulla "tavoletta di Strassburgo", la più antica testimonianza di algebra che abbiamo al momento.
Siamo nel 1800 a.C., civiltà Babilonese, quasi 4000 anni fa.

"La somma delle aree di due quadrati è 1000.
Il lato di un quadrato è di 10 unità minore dei due terzi del lato dell’altro quadrato.
Quanto misurano i lati dei due quadrati?”

24. Formati televisivi

Un’immagine registrata in formato 4:3 (rapporto tra larghezza e altezza dello schermo) vista su un televisore di formato 4:3 e su uno di formato 16:9.
In questo caso per non distorcere l’immagine, sul televisore 16:9 vengono aggiunte delle strisce nere verticali.

Quanto sono larghe queste strisce su un televisore da 40’’ di diagonale?

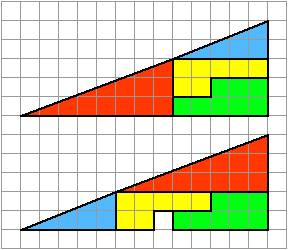
25. La sparizione dell'area

Un altro classico.
Le due figure sono composte dagli stessi quattro pezzi.
Ma nella seconda manca un quadratino.
La sua area è quindi minore. Perché?

26. Accostamento di numeri di tre cifre

302 (scegli un numero di tre cifre)
302'302 (ripetilo due volte, formando un numero di 6 cifre)
302'302 : 13 = 23'754 (dividi per 13)
23'754 : 11 = 2'114 (dividi per 11)
2'114 : 7 = 302 (dividi per 7)
(ottieni il numero da cui sei partito)

Spiega come mai succede questo per tutti i numeri di tre cifre.

27. Quadrati sulla scacchiera

Un altro classico.
Quanti quadrati si possono formare su una scacchiera?

28. La figura che cresce

Quanti quadratini avrà la centododicesima figura?
Domanda bonus: perché Gauss non può giocare?

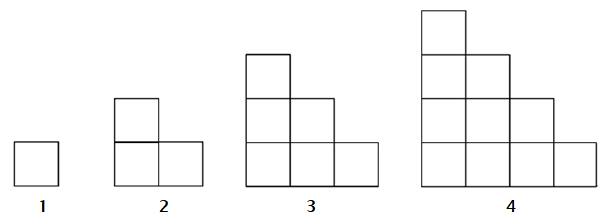
29. Completa la frase

"Questa frase contiene ...................... lettere"

Completare con un numero scritto in lettere, in modo che la frase risulti vera.

30. Tre dieci per un sei

Usando tre volte il numero 10, costruire un'espressione che dia come risultato 6.
Operazioni ammesse: addizione, sottrazione, divisione, moltiplicazione, radice quadrata, fattoriale.
Parentesi quante ne volete.

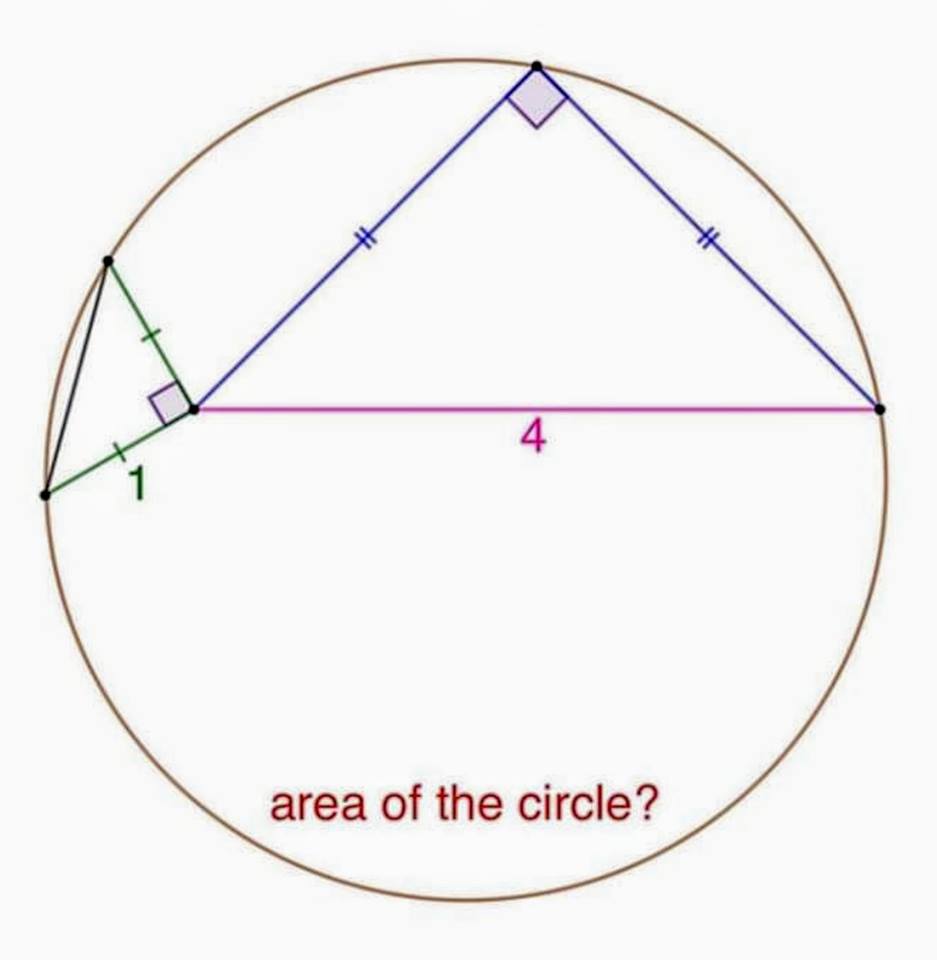
31. Triangoli nel cerchio

Trovare l'area del cerchio nella situazione illustrata qui sotto.
La risoluzione dell'equazione risolutiva, perlomeno quella della soluzione che conosco, va un po' oltre le conoscenze della scuola media.
Nel caso non si riesca a risolverla, ci si può affidare a un risolutore online come Wolfram Alpha.

32. Quadrati sui puntini

Quanti diversi quadrati, con tutti i vertici sui puntini, si possono disegnare su questa griglia?.

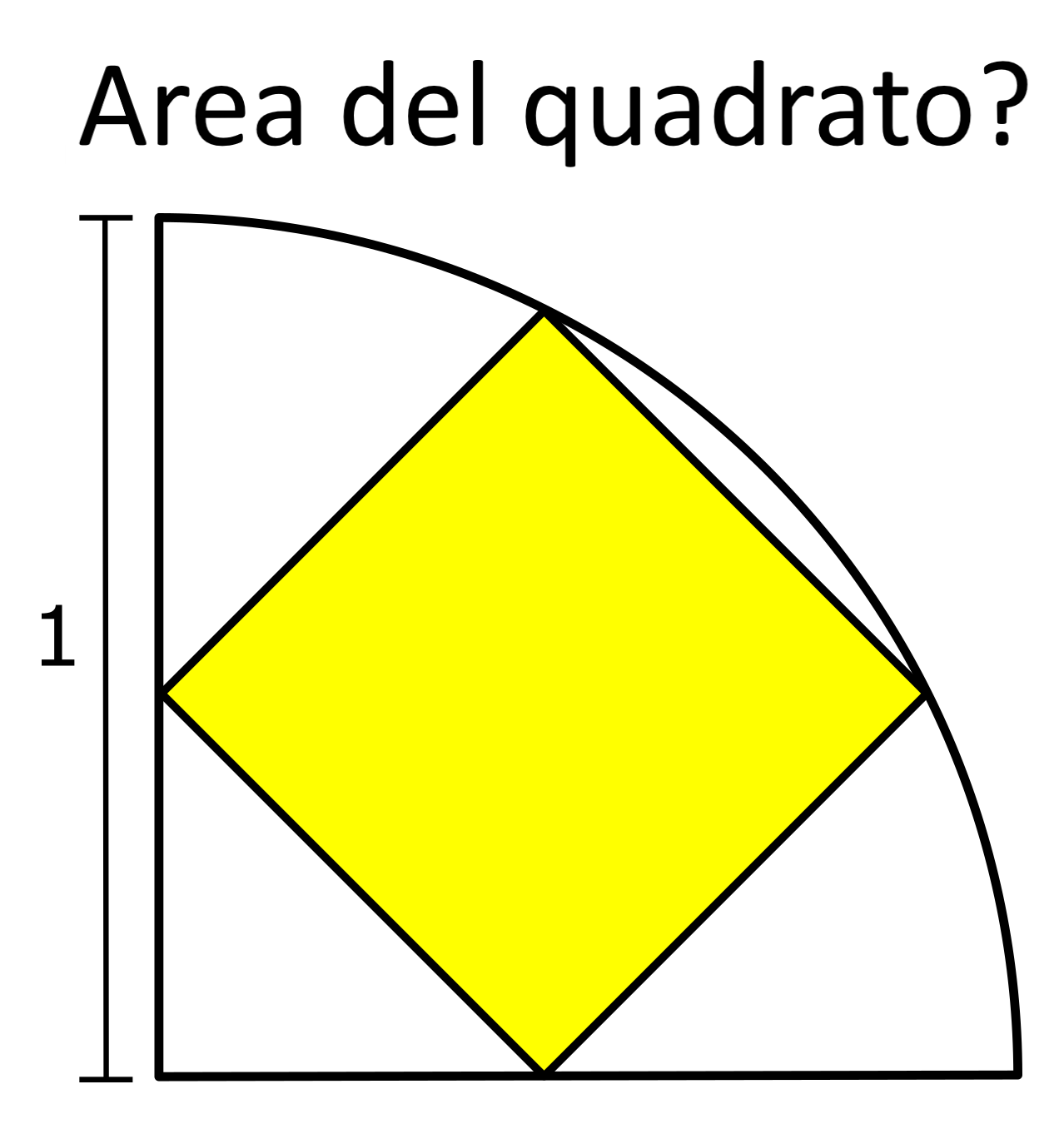
33. L'area del quadrato

34. Trova il rapporto tra il raggio del cerchio rosso e quello del cerchio verde (San Gaku).

I San Gaku (o Sangaku) sono problemi solitamente di geometria rappresentati su tavolette di legno e donati come offerta a santuari e templi durante il periodo Edo in Giappone.